संख्या पद्धति (Number System in Hindi) से सम्बन्धित परीक्षाओं में पीछे जाने वाले सामान्य प्रश्न जैसे – संख्या पद्धति के सूत्र, pdf downloadm, संख्या पद्धति के प्रकार, संख्या पद्धति के सभी सूत्र, sankhya paddhati in hindi pdf, संख्या प्रणाली गणित, sankhya paddhati formula, सबसे बड़ी प्राकृतिक संख्या, पूर्ण संख्या किसे कहते हैं, क्या सभी प्राकृतिक संख्या पूर्ण संख्या है, प्राकृत संख्या किसे कहते हैं परिभाषा, प्राकृत संख्या किसे कहते हैं उदाहरण सहित समझाइए, प्रत्येक प्राकृतिक संख्या एक पूर्ण संख्या होती है, 1 से 100 तक अभाज्य संख्या, सह अभाज्य संख्या किसे कहते है, अभाज्य संख्या निकालने का फार्मूला, 1 से 500 तक अभाज्य संख्या, संपूर्ण संख्या भाज्य अभाज्य संख्या, विषम अभाज्य संख्या, पूर्ण संख्याएँ कक्षा 6, पूर्ण संख्या प्राकृतिक संख्या, प्राकृत संख्या और पूर्ण संख्या, प्राकृतिक और पूर्ण संख्या, प्राकृत और पूर्ण संख्या, पूर्ण संख्या के नियम,पूर्ण संख्या के गुण, संख्या पद्धति पर आधारित प्रश्न, योग, अंतर और गुणा पर आधारित प्रश्न, क्रमागत संख्याओं पर आधारित प्रश्न, विभाज्यता पर आधारित प्रश्न PDF, स्थानीय मान के प्रश्न, अभाज्य गुणनखंड के प्रश्न, शेषफल पर आधारित प्रश्न PDF आदि के बारे में इस पोस्ट में विस्तार से जानकारी मिलेगी ।
या किसी भौतिक राशि के परिणामों को बोध कराने के लिए जिस पद्धति का प्रयोग किया जाता हैं,“संख्या पद्धति” कहलाती है।
अंक(Digit) – गणित में 0 से लेकर 9 तक के संकेतों को अंक कहते हैं
- इनकी इनकी संख्या 10 होती है। जैसे – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
संख्या(Number) – एक से अधिक अंकों को मिलाने पर संख्या का निर्माण होता है
- इनकी संख्या अनन्त होती है
- जैसे – 123, 241, 2375,855,5833
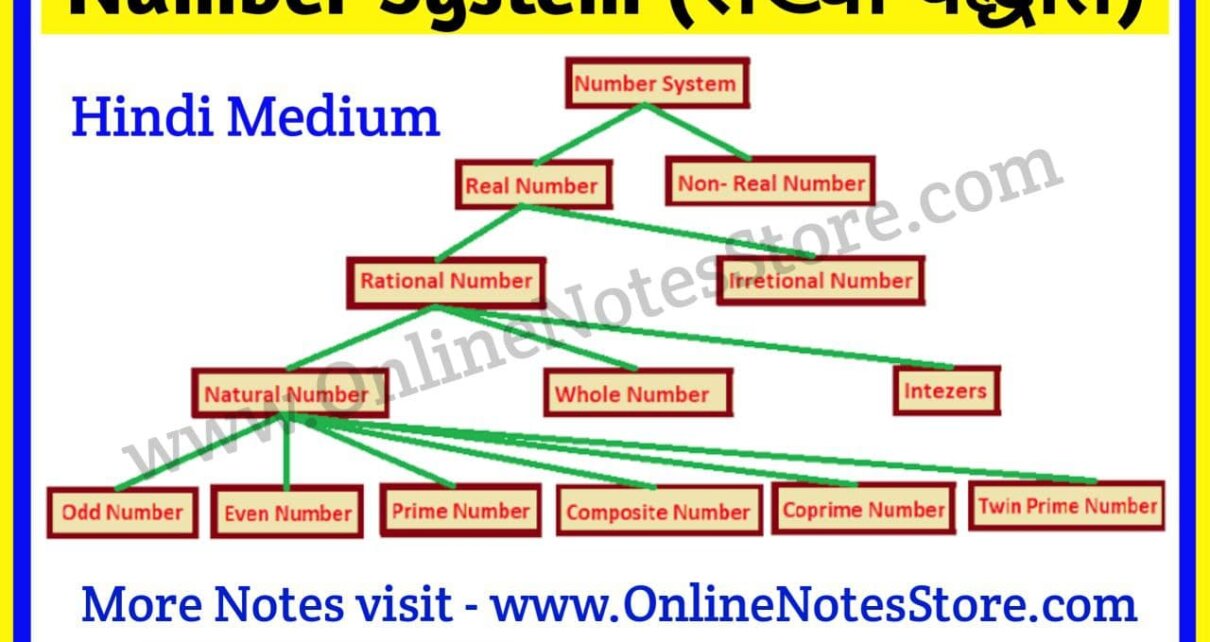
संख्याओं के प्रकार (Types of Numbers) निम्नलिखित है –
- प्राकृतिक संख्या (Natural Number):–गिनती की संख्याओं को प्राकृतिक संख्या कहते हैं अथवा ऐसी संख्याएँ जो 1 से शुरू होकर अनन्त तक चलती है, प्राकृतिक संख्याएँ कहलाती है ।
- प्राकृतिक संख्या को N प्रकट करते हैं।
- 1 सबसे छोटी प्राकृतिक संख्या है।
- पाइनोस के अनुसार वे संख्याए जिनसे वस्तुओं को गिना जा सकता है,प्राकृतिक संख्याएँ कहलाती है ।
जैसे – N = { 1, 2, 3, 4, 5, 6 ………… }
संक्रिया आधारित प्रश्न
प्रश्न-1 यदि a और b कोई दो प्राकृतिक संख्याएँ हो, तो
A- a + b सदैव प्राकृतिक संख्याएँ होगी ✔
B- a – b सदैव प्राकृतिक संख्याएँ होगी ×
C- a × b सदैव प्राकृतिक संख्याएँ होगी ✔
D- a ÷ b सदैव प्राकृतिक संख्याएँ होगी ×

2. पूर्ण संख्याऐं (Whole Numbers):- यदि प्राकृतिक संख्याओं में 0 को शामिल कर लिया जाए तो जो संख्याएँ प्राप्त होती है, पूर्ण संख्याएँ कहलाती है । –
- पूर्ण संख्या को W से प्रकट करते हैं।
- 0 सबसे छोटी पूर्ण संख्या है।
- 0 ऐसा अंक है जो W को N से अलग करता है।
- सभी प्राकृतिक संख्याएं पूर्ण संख्या है, लेकिन सभी पूर्ण संख्या प्राकृतिक संख्या नहीं है। जैसे – 0
जैसे – W = { 0, 1, 2, 3, 4, 5, 6 ………… }
नोट – पूर्ण संख्या(Perfect Number)– ऐसी संख्याएँ जिनके गुणनखण्डों का योग (स्वयं को छोडकर) करने पर वही संख्या प्राप्त हो, पूर्ण संख्या(Perfect Number) कहलाती है
जैसे – 6, 28,496, 8128
- 28 के गुणनखंड = 1×28, 2×14, 4×7 = 1, 2, 4, 7, 14, 28 = 1+2+4+7+14=28
3. पूर्णांक संख्याएँ (Integers Number):- पूर्ण संख्याओं में ऋणात्मक संख्याएँ शामिल करने पर जो संख्याएँ प्राप्त होती है, पूर्णांक संख्याएँ कहलाती है या वे संख्याएँ जो -∞ से +∞ तक चलती है उन्हें पूर्णांक संख्याएँ कहते- है
- पूर्णांक संख्याओं को Z से प्रकट करते हैं।
- Zealean नामक जर्मन गणितज्ञ ने सबसे पहले पूर्णांक संख्याओं के बारे में बताया
- 0 समस्त ऋणात्मक पूर्णांक संख्याओं से बड़ा होता है तथा समस्त धनात्मक पूर्णांक संख्याओं से छोटा होता है
जैसे – Z = { …..….-5, -4, -3, -2, -1,0, 1, 2, 3, 4, 5 ………… }
संक्रिया आधारित प्रश्न –
प्रश्न- यदि a और b कोई दो पूर्णांक संख्याएँ हो, तो
A- a + b सदैव पूर्णांक संख्याएँ होगी ✔
B- a – b सदैव पूर्णांक संख्याएँ होगी ✔
C- a × b सदैव पूर्णांक संख्याएँ होगी ✔
D- a ÷ b सदैव पूर्णांक संख्याएँ होगी ×

4. सम संख्याएँ (Even umbers):– वे संख्याएँ जो 2 से पूरी पूरी विभाजित हो “सम संख्याएँ” कहलाती है ।
- सम संख्याओं को E से प्रकट करते है ।
- 2 सबसे छोटी सम संख्या है ।
- सम संख्याओं का इकाई अंक 0, 2, 4, 6 या 8 होता है।
- नोट – 0 एक सम संख्या है ।
जैसे-: 2, 4, 6, 8, 10, 12,…….
5.विषम संख्याऐं (Odd numbers):– वे संख्याएँ जो 2 से पूरी पूरी विभाजित नही हो “विषम संख्याएं” कहलाती है।
- विषम संख्याओं को O से प्रकट करते है ।
- 1 सबसे छोटी विषम संख्या है ।
- विषम संख्याओं का इकाई अंक 1, 3, 5, 7, या 9 होता है ।
जैसे:-1, 3, 5, 7, 9,…….
6. परिमेय संख्याएँ (Rational Number):- वे संख्याएँ जिन्हें p/q के रुप में लिखा जा सकता है परिमेंय संख्याएँ (Rational Number) कहलाती है, जहाँ p और q पूर्णांक संख्याएँ है तथा q≠0 है अर्थात q का मान 0 के बराबर नही होगा ।
- परिमेय संख्याओं को “Q” से प्रकट करते है।

संक्रिया आधारित प्रश्न –
प्रश्न- यदि a और b कोई दो परिमेय संख्याएँ हो, तो
A- a + b सदैव परिमेय संख्याएँ होगी ✔
B- a – b सदैव परिमेय संख्याएँ होगी ✔
C- a × b सदैव परिमेय संख्याएँ होगी ✔
D- a ÷ b सदैव परिमेय संख्याएँ होगी ×

संक्रिया आधारित प्रश्न –
प्रश्न- यदि a और b कोई दो वास्तविक संख्याएँ हो, तो
A- a + b सदैव वास्तविकसंख्याएँ होगी ✔
B- a – b सदैव वास्तविक संख्याएँ होगी ✔
C- a × b सदैव वास्तविक संख्याएँ होगी ✔
D- a ÷ b सदैव वास्तविक संख्याएँ होगी ×

7. अवास्तविक (Non – Real Number) या काल्पनिक संख्या(Imaginary Number) – वे संख्याएँ जिनका वर्ग करने पर एक ऋणात्मक संख्या प्राप्त होती है, अवास्तविक संख्या (Non – Real Number) कहलाती है । ऐसी संख्याओं की केवल कल्पना ही की जा सकती है ।
जैसे – √-2, √-3, √-6, √-9,√-25

8. समिश्र संख्या (Complex Number) – जब किसी वास्तविक संख्या में किसी काल्पनिक संख्या को जोड़ा या घटाया जाता है तो प्राप्त परिणाम समिश्र संख्या कहलाती है
जैसे – 3-√-2, 5+√-7
9. अभाज्य संख्या (Prime Numbers):– वे संख्याएँ जिनमें स्वयं तथा 1 को छोडकर किसी अन्य संख्या का भाग नही जाता है ,अभाज्य संख्याएं कहलाती है। अथवा वे संख्याएँ जिनके केवल और केवल 2 गुणनखंड हो,अभाज्य संख्याएं कहलाती है।
जैसे:- 2, 3, 5, 7, 11, 13…..
- अभाज्य संख्याओं को रूढ़ संख्याएँ भी कहते है
- 1 न तो भाज्य संख्या है, और न ही अभाज्य संख्या।
- 2 सबसे छोटी अभाज्य संख्या है
- 2 एक मात्र ऐसी सम संख्या है,जो अभाज्य संख्या भी है।
- 3 सबसे छोटी विषम अभाज्य संख्या है।
- 1 से 25 तक अभाज्य संख्याएँ – 9
- 1 से 30तक अभाज्य संख्याएँ – 10
- 1 से 50 तक अभाज्य संख्याएँ – 15
- 25 से 50 तक कुल अभाज्य संख्या-6
- 50 से 100 तक कुल अभाज्य संख्या-10
- 1 से 75 तक अभाज्य संख्याएँ – 21
- 1 से 100 तक अभाज्य संख्याएँ – 25
- 1 से 100 तक की अभाज्य संख्याएं – 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
नोट – कोई संख्या अभाज्य है या नही इसकी जाँच करने के लिए जिस किसी संख्या की हमें जाँच करनी हो तो
- उस संख्या से छोटी सबसे निकट पूर्ण वर्ग संख्या का वर्गमूल ज्ञात करें
- उस वर्गमूल से छोटी सभी अभाज्य संख्याओं का भाग दी गई संख्या में दें
- यदि किसी अभाज्य संख्या का भाग नही जाता है तो दी गई संख्या अभाज्य संख्या है
जैसे – 331
- 331 से छोटी निकटतम पूर्ण वर्ग संख्या – 324
- 331 का वर्गमूल = 18
- 18 से छोटी अभाज्य संख्याएं =2, 3, 5, 7, 11, 13, 17
- 331,18 से छोटी किसी भी अभाज्य संख्या से विभाजित नही है अतः 331 अभाज्य संख्या है
10. भाज्य संख्या (Composite Number):– वे संख्याएँ जिनमें स्वयं तथा 1 को छोडकर किसी अन्य संख्या का भी भाग जाता है ,भाज्य संख्याएं कहलाती है। अथवा वे संख्याएँ जिनके कम से कम 3 गुणनखंड हो,भाज्य संख्याएं कहलाती है।
जैसे:- 4, 6, 9, 10, 12 ……
- सबसे छोटी भाज्य संख्या 4 है
- सबसे छोटी विषम भाज्य संख्या 9 है।
- 1 से 25 तक अभाज्य संख्याएँ – 15
- 1 से 30तक भाज्य संख्याएँ – 19
- 1 से 50 तक भाज्य संख्याएँ – 34
- 1 से 75 तक भाज्य संख्याएँ – 53
- 1 से 100 तक भाज्य संख्याएँ – 74
नोट – सबसे छोटी भाज्य संख्या, सबसे छोटी अभाज्य संख्या का पूर्ण वर्ग है जैसे – 4 =
- सबसे छोटी विषम भाज्य संख्या, सबसे छोटी विषम अभाज्य संख्या का पूर्ण वर्ग है जैसे – 9 =
11. सहअभाज्य संख्याएँ (Prime Numbers) तथा आपेक्षित अभाज्य संख्या (Relatively Prime Number)-
| क्रम सं. | सहअभाज्य संख्याएँ (Prime Numbers) | आपेक्षित अभाज्य संख्या (Relatively Prime Number) |
| 1. | वे संख्या युग्म जिनका महत्तम समापवर्तक(HCF) 1 हो | वे संख्या युग्म जिनका महत्तम समापवर्तक(HCF) 1 हो |
| 2. | (यदि दोनों संख्याएँ एक साथ ऑप्शन में हो तो )
इसमें संख्या युग्म केवल अभाज्य संख्याओं के ही बनाते हैं |
इसमें संख्या युग्म भाज्य, अभाज्य संख्याओं के बनाते हैं |
| 3. | जैसे – (2,3),(5,7),(3,5) | जैसे – (25,36),(4,9,11),(9,14) |
12. युग्म-अभाज्य संख्याएँ(Twin Prime Number): ऐसी अभाज्य संख्याओं के संख्यायुग्म जिनके बीच का अंतर 2 हो ‘Twin Prime Number’ कहलाती हैं।
जैसे- (11, 13), (5,7),(17,19), (29,31), (59,61), (71,73)
13. रामानुजम संख्या – वह छोटी से छोटी संख्या जिसे दो अलग – अलग प्रकार से घनों के योग के रूप में लिख जा सकता है, रामानुजम संख्या कहलाती है

14. अत्रिभाज्य संख्याएँ (Prime Triplet Number):- वे तीन प्राकृतिक संख्याएँ जिनका महत्तम समापवर्तक (H.C.F) 1 हो, अत्रिभाज्य संख्याएँ कहलाती है ।
जैसे:- 8 , 9 तथा 25
दशमलव भिन्न (Decimal Fraction):- ऐसी भिन्नात्मक संख्याएँ जिनका हर 10 हो या 10 की घात के रूप में हो उसे दशमलव भिन्न कहते हैं ।
जैसे: -7/10, 17/100, 11/1000, 3/10000, …… इत्यादि
संख्याओं का दशमलव प्रसार
जब किस संख्या का अन्य संख्या में भाग दिया जाता है तो भागफल दो प्रकार का प्राप्त होता है। इन संख्याओं का दशमलव प्रसार (Decimal Expansion of Rational Number) या तो सांत दशमलव प्रसार होता है या असांत आवर्ती दशमलव प्रसार होता है। एक परिमेय संख्या का सांत दशमलव प्रसार कब होता है और कब यह असांत आवर्ती दशमलव प्रसार होता है।
प्रमेय 1 – यदि x एक परिमेय संख्या है जिसका दशमलव प्रसार सांत है, तो x को p/q के रूप में व्यक्त किया जा सकता है, जहाँ p और q सहअभाज्य संख्याएँ हैं और q का अभाज्य गुणनखंड 2n×5m के रूप का है, जहाँ n और m ऋणेतर पूर्णांक संख्याएँ हैं।
- 33/2×52 = 27/2×52
अंश और हर को 2 से गुणा करने पर
= 27×2/2×2×52
= 54/22×52
= 54/(2×5)2
= 54/(10)2
= 54/100
= 0.54 or 0.540
प्रमेय 2 – यदि x, p/q के रूप की एक ऐसी परिमेय संख्या है, कि q का अभाज्य गुणनखंड 2n×5m के रूप का है, जहाँ n और m ऋणेतर पूर्णांक संख्याएँ हैं, तो x का दशमलव प्रसार, सांत दशमलव प्रसार होता है।
- 1/3
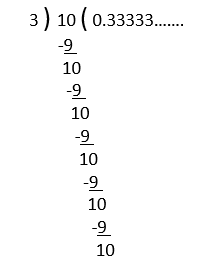
2. 7/6
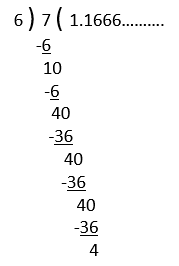
प्रमेय – यदि x, p/q के रूप की एक ऐसी परिमेय संख्या है, कि q का अभाज्य गुणनखंड 2n×5m के रूप का नहीं है, जहाँ n और m ऋणेतर पूर्णांक संख्याएँ हैं, तो x का दशमलव प्रसार, असांत आवर्ती दशमलव प्रसार होता है।
सम्बन्धित उदाहरण
उदाहरण 1. लंबी विभाजन प्रक्रिया किए बिना निम्नलिखित का दशमलव प्रसार लिखिए।
i. 17/3125 ii. 77/210
हल – i. 17/3125 = 17/20×55
- हर 3125, 2n×5m के रूप का है, इसलिए , 17/3125 का दशमलव प्रसार सांत है।
ii. 77/210 = 77/2×3×5×7
- हर 210, 2n×5m के रूप का नहीं है, इसलिए, 77/210 का दशमलव प्रसार, असांत आवर्ती है।
उदाहरण 2. दशमलव प्रसार की सहायता से बताइए कि दी गई संख्याएँ, परिमेय संख्याएँ हैं या अपरिमेय संख्याएँ है।
i) 123.1236289476……. ii) 34.654321 iii) 0.324532453245………..
हल – i) 123.1236289476…….
इस संख्या का दशमलव प्रसार, असांत अनावृत्ति है इसलिए यह संख्या एक अपरिमेय संख्या है।
ii) 34.654321
इस संख्या का दशमलव प्रसार सांत है इसलिए यह संख्या एक परिमेय संख्या है।
iii) 0.324532453245………..
इस संख्या का दशमलव प्रसार असांत आवर्ती है अतः यह संख्या एक परिमेय संख्या है।
नोट –
1. उपरोक्त स्पष्टीकरणों से पता चलता है कि प्रत्येक परिमेय संख्या का दशमलव प्रसार या तो सांत या असांत आवर्ती होता है।
2. यदि कोई ऐसी संख्या है जिसका दशमलव प्रसार असांत अनावर्ती है तो वह संख्या अपरिमेय संख्या कहलाती है।
संख्याओं / संख्या पद्धति के महत्वपूर्ण गुण / महत्वपूर्ण तथ्य ( Number System Important Fact) –
- 2 एकमात्र ऐसी संख्या जो अभाज्य है एवं सम संख्या भी है । 2 के अतिरिक्त सभी संख्याएँ भाज्य है ।
- वे दो अभाज्य संख्याएँ जिनके बीच केवल एक सम संख्या होती है , अभाज्य जोड़ा कहलाती है , जैसे – 5 व 7 , 3 व 5 , 11 व 13 , 17 व 19 , 29 व 31 आदि ।
|
सत्य ↓
|
प्राकृतिक संख्या | असत्य
↑ |
| पूर्ण संख्या | ||
| पूर्णांक संख्या | ||
| परिमेय संख्या | ||
| वास्तविक संख्या | ||
| प्रत्येक प्राकृत संख्या – पूर्ण, पूर्णाक, परिमेय एवं वास्तविक होती हैं । – सत्य |
प्रत्येक वास्तविक संख्या परिमेय संख्या होती है। – असत्य |
- सभी प्राकृत संख्याएँ, पूर्ण, पूर्णाक, परिमेय एवं वास्तविक होती हैं ।
- सभी पूर्ण संख्याएँ, पूर्णांक, परिमेय एवं वास्तविक होती हैं ।
- सभी पूर्णाक, परिमेय एवं वास्तविक होते हैं ।
- सभी पूर्णांक, परिमेय एवं अपरिमेय संख्याएँ वास्तविक होती हैं ।
- अभाज्य ( रूढ़ ) एवं यौगिक , सम तथा विषम संख्या होती हैं।
- सभी पूर्णाक, परिमेय एवं अपरिमेय संख्याएँ ऋणात्मक एवं धनात्मक दोनों होती हैं ।
- प्राकृत (अभाज्य , यौगिक , सम एवं विषम) एवं पूर्ण संख्याएँ कभी भी ऋणात्मक नहीं होती हैं । अर्थात धनात्मक होती है ।
- भिन्न संख्याएँ परिमेय होती हैं ।
- 2 के अतिरिक्त सभी अभाज्य ( रूढ़ ) संख्याएँ विषम होती हैं ।
- 0 ऋणात्मक एवं धनात्मक नहीं है ।
- शून्य ( 0 ) में किसी भी संख्या का भाग देने पर शून्य प्राप्त होता है । अतः 0/a = 0 ( यहाँ a वास्तविक संख्या है ) ।
- किसी भी संख्या में शून्य का भाग देना परिभाषित नहीं है अर्थात् यदि किसी भी संख्या में शून्य का भाग देते हैं , तो भागफल अनन्त ( Infinite या Non Defined ) आता है ।
- अतः a/0 = ∞ ( Infinite ) ।
- किसी संख्या में किसी अंक का जो वास्तविक मान होता है , उसे जातीय मान कहते हैं , जैसे – 3256 में 2 का जातीय मान 2 है ।
- किसी संख्या में किसी अंक का स्थान के अनुसार जो मान होता है उसे उसका स्थानीय मान कहते हैं , जैसे – 3256 में 2 का स्थानीय मान 200 है ।
- दो परिमेय संख्याओं का योगफल अथवा गुणनफल सदैव एक परिमेय संख्या होती है ।
- दो अपरिमेय संख्याओं का योगफल अथवा गुणनफल कभी परिमेय संख्या तथा कभी अपरिमेय संख्या होता है ।
- एक परिमेय संख्या तथा एक अपरिमेय संख्या का गुणनफल अथवा योगफल सदैव एक अपरिमेय संख्या होता है ।
- π एक अपरिमेय संख्या है । क्योंकि π का मान 3.14159…… जो कि असांत आवृति होता है।
- दो परिमेय संख्याओं या दो अपरिमेय संख्याओं के बीच अनन्त परिमेय संख्याएँ या अनन्त अपरिमेय संख्याएँ हो सकती हैं ।
- परिमेय संख्या को दशमलव निरूपण या तो सीमित होता है या असीमित आवर्ती होता है , जैसे – i. 3/4 = 0.75 ( सीमित ) ii. 11/3 = 3.666 ( असीमित आवर्ती )।
- अपरिमेय संख्या का दशमलव निरूपण अनन्त व अनावर्ती होता है , जैसे – √3 , √2 ।
- प्रत्येक सम संख्या का वर्ग एक सम संख्या होती है तथा प्रत्येक विषम संख्या का वर्ग एक विषम संख्या होती है ।
संख्याओं / संख्या पद्धति के महत्वपूर्ण सूत्र ( Number System Important Formulas) –
- प्रथम n प्राकृतिक संख्याओं का योग SnE = n (n + 1 ) /2 होता है ।
- प्रथम n सम संख्याओं का योग SE = n ( n + 1 ) होता है ।
- प्रथम n विषम संख्याओं का योग S0 = n2 होता है ।
- किसी भी पहाड़े का योग उस संख्या के पहाड़े के 55 गुने के बराबर होता है ।
2 के पहाड़े का योग – 2+4+6+8+10+12+14+16+18+20+ = 110 = 2 × 55
अर्थात् n के पहाड़े का योगफल = 55n
- 1 से n तक के पहाड़े का योगफल = 55 [ n (n + 1 )/2 ]
- प्राकृतिक संख्याओं के वर्गों का योगफल अर्थात् 12 + 22 + 32 + . . . + n2 = n/6( n + 1 ) ( 2n + 1 ) होता है ।
- n प्राकृतिक संख्याओं के घनों का योगफल अर्थात् 13 + 23 + 33 + 43 + . . . + n3 = [n (n + 1)/2 ]2 होता है ।
- n प्राकृतिक सम संख्याओं के वर्गों का योगफल अर्थात् 22 + 42 + 6 2+ . . . + n2 = 2n/3( n + 1 ) ( 2n + 1 )
- n प्राकृतिक सम संख्याओं के घनों का योगफल अर्थात् 23 + 43 + 63 + . . . + 3 = 2n2 ( n + 1 )2 आदि ।
संख्या पद्धति के महत्वपूर्ण प्रश्न उत्तर ( Number System Important Questions) –
प्रश्न – सबसे छोटी अभाज्य संख्या कौनसी है ?
उत्तर – 2
प्रश्न – एक मात्र ऐसी संख्या जो सम संख्या है,जो रूढ़ संख्या भी है
उत्तर – 2
प्रश्न – सबसे छोटी विषम अभाज्य संख्या कौनसी है
उत्तर – 3
प्रश्न – सबसे छोटी भाज्य संख्या कौनसी है?
उत्तर – 4
प्रश्न – सबसे छोटी विषम भाज्य संख्या कौनसी है?
उत्तर – 9
प्रश्न – 1 से 100 तक कुल कितनी अभाज्य संख्याएँ हैं ?
उत्तर – 25
प्रश्न – 1 से 50 तक कुल कितनी अभाज्य संख्याएँ हैं ?
उत्तर – 15
प्रश्न – 1 से 25 तक कुल कितनी अभाज्य संख्याएँ हैं ?
उत्तर – 9
प्रश्न – 25 से 50 तक कुल कितनी अभाज्य संख्याएँ हैं ?
उत्तर – 6
प्रश्न – 50 से 100 तक कुल कितनी अभाज्य संख्याएँ हैं ?
उत्तर – 10
प्रश्न – अंको की कुल संख्या कितनी होती है ?
उत्तर – 10
प्रश्न – एक अंकीय संख्याएँ कितनी होती है ?
उत्तर – 9
प्रश्न – दो अंकीय संख्याएँ कितनी होती है ?
उत्तर – 90
प्रश्न – तीन अंकीय संख्याएँ कितनी होती हैं ?
उत्तर – 900
प्रश्न – चार अंकीय संख्याएँ कितनी होती हैं ?
उत्तर – 9000
प्रश्न – 1 से 100 तक की संख्याओ में शून्य के कितने अंक होते हैं ?
उत्तर – 11
प्रश्न – 1 से 100 तक की संख्याओ में एक के कितने अंक होते हैं ?
उत्तर – 21
प्रश्न – 1 से 100 तक की संख्याओ में 2 से 9 तक प्रत्येक अंक कितनी बार आते है ?
उत्तर – 20
प्रश्न – 1 से 100 तक की संख्याओ में कुल कितने अंक होते हैं ?
उत्तर – 192
Explaination
1 से 100 तक इकाई अंक = 100
1 से 100 तक दहाई अंक = 91
1 से 100 तक सैकड़ा के अंक = 1
प्रश्न – तीन अंको की कितनी संख्या है संभव है ?
उत्तर – 900
trick – तीन अंको की कुल संख्या = तीन अंको की सबसे बड़ी संख्या- दो अंको की सबसे बड़ी संख्या
प्रश्न – एक परिमेय संख्या और एक अपरिमेय संख्या का गुणनफल क्या होता है ?
उत्तर – अपरिमेय संख्या
प्रश्न- संख्या 1.235 जिनमे 35 के ऊपर बार का चिन्ह है को p/q के रूप में व्यक्त कीजिये जहाँ p, q पूर्णाक तथा q, 0 के बराबर नही है?
उत्तर – 1223/990
प्रश्न- 51+52+…………..+100=?
उत्तर – 3775
प्रश्न- यदि n एक धनात्मक पूर्णांक है तो 3 की घात 4n–4 की घात 3n सदैव निम्नलिखित में से किस संख्या से पूर्णतया विभाजित होगा?
उत्तर – 17
- संख्या पद्धति | Number System
- गणितीय महत्वपूर्ण संकेत एवं नाम | Math Symbol in Hindi
- मन की गणित Book PDF Free Download
- Maths Handwritten Notes PDF
- Polygon Maths Handwritten Notes by Ankur Yadav